Accuracy
Watch this as a video
The basics
Imagine you are measuring the width of your bedroom before you go shopping for wall paper. You may choose to use meter sticks and count how many fit between the walls. Sure, there may be a bit of space left over, but you may feel this is good enough. For extra precision you may choose to use a measuring tape, getting the distance correct to a centimetre or millimetre. There are devices now that use lasers to get even more precision.
The point is, you need to make a decision when you measure something how precise you want that measurement to be.
There are three types of rounding you should be familiar with, nearest ‘something’, decimal places and significant figures.
Nearest ‘something’
If 855.74 is rounded to the nearest integer (whole number) we are looking to get rid of any decimals we have in the number. Draw the number on a place value table and draw a line after the ones column.
There are two numbers that 855.74 could round to. 855 or 856. To decide which it is closer to, we look at the number to the RIGHT of the line we drew. This is our decider number. If it is 5 or more, round up. Less than 5 and we round down.
The number in the tenths column is 7. This is ‘5 or more’ so we will round up to 856.

Decimal places
Decimal places count how many digits we want after the decimal point. One decimal place, will give us one digit after the point, two decimal places will give us two, etc.
If 855.74 is rounded to one decimal place we will draw a line after the tenths column.
There are two numbers that 855.74 could round to. 855.7 or 855.8. The number in the hundredths column is 4. This is ‘less than 4’, so our number will round down to 855.7.

Significant figures
Significant figures work in almost the same way as decimal places, but instead of counting from the decimal point, we start from the beginning of the number. One significant figure will leave us with one digit, two significant figures will leave us with two digits, etc. We will soon discover, however, that there is something else we need to be careful of.
We will draw the line after the 8 for 855.74 because this is the first digit. The decider number is 5, so the 8 will round to a 9. So our answer is 9? NO!
Imagine someone says that a house is 855.74cm tall. Would you say, “that’s roughly 9 cm!”
The bit we need to remember is when we round numbers, we do NOT remove the numbers to the right of our line. We reset them back to 0. 855.74 to one decimal place was 855.70, but we just did not need to write the 0 because it is not a place holder.
855.74 to one significant figure will therefore give us 900.00, but we can remove the zeros after the decimal points because these are not placeholders. So our answer is 900.

Try our paper on this
Estimate
Imagine you are buying three tubes of toothpaste at £3.99 each. To work out the total, you would likely do 3 times 4, to estimate the price at roughly £12. This is estimating.
In maths it is generally acceptable, if there are no other factors at play, to round numbers to one significant figure when estimating.
Lets estimate an answer to this calculation.
2.7 ×17.90.547
We start by rounding each number to one significant figure. 2.7 will become 3, 17.9 will become 20 and 0.547 will round to 0.5. We now have this:
3 × 200.5
This is much easier for us to do in our head! 3 times 20 is 60, 60 divided by a half is 120.
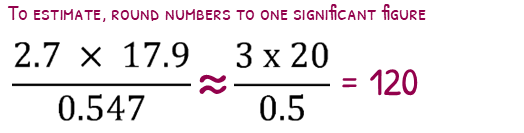
Under or over?
It is always important to keep track of the effects of our estimating. Either our number will be lower than the correct answer, or higher than it. The real answer is 96.66, so our answer is an overestimate.
If we didn’t have a calculator, we can see how we rounded each number. The numerators were both rounded up and the denominator was rounded down, so our estimate will be larger than the real answer, so is an overestimate.
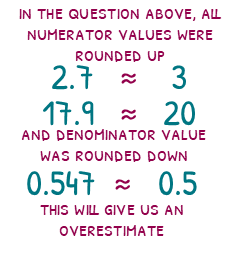
Special cases
The purpose of estimation is to give us a quick way to work out roughly what an answer is. Rounding a square root to one significant figure will not help us. If you do not know what the square root of 28 is in your head, chances are you don’t know 30!
With square roots, its more helpful to round to the nearest square number. 28 is very close to 25, so the square root of 28 is roughly the square root of 25, which is 5.
√28≈√25
Very rarely you may be asked to make estimate with π. If you have a calculator π can be estimated to 3.14, if you do not then 3 should be good enough. Note, it is ALWAYS better to leave your answer in terms of π if you can!
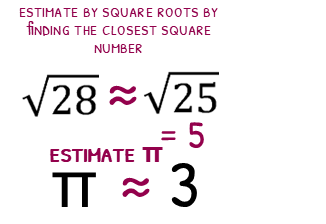
Try our paper on this
Error intervals
When we come across numbers that have been rounded, it is often important to know what the numbers could have been before rounding. A common way of doing this is with error intervals.
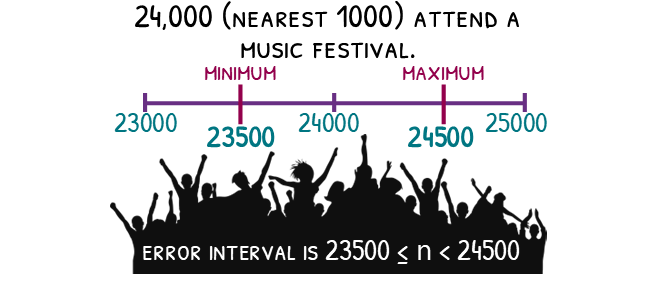
Imagine 24,000 people attended a music festival, but this number was rounded to the nearest 1000. To find the error interval, imagine what the next number DOWN that it could have rounded to. This would have been 23000. Our minimum value will be half way between these numbers, or 23500. Now imagine the next number UP it could have rounded to. This would have been 25000. Our maximum value will be half way between these numbers, or 24500.
This hasn’t given us our interval yet though. The interval is create by giving the value a letter, n for example. We can now write an inequality to show the range that the original number could have been. It could have been equal to 23500, but it could not have been equal to 24500 (otherwise it would have rounded to 25000).
Our error interval will therefore be 23500 ≤ n < 24500
Truncated numbers
We may need to find an error interval for a number than has been truncated, and not rounded. When a number has been truncated, the end of the number has simply been chopped off!
Imagine a calculator has a note covering the last two digits of a five digit number. We can see that the first three digits are 408.
The lowest possible digits that could be hiding under the note are 0 and 0. This makes our lowest value 40800.
The largest digits are 9 and 9, making our largest value 40899.
Our error interval will therefore be 40800 ≤ n < 40899

Try our papers on this
- Finding Minimum and Maximum Values Paper (foundation)
- Error Intervals Paper (foundation)
- Finding Bounds Paper (higher)
Calculating with bounds (higher only)
The minimum and maximum values are known as the lower and upper bounds. We can use the bounds in calculations to find maximum and minimum answers.
Imagine we have a rectangle that is 4cm by 3cm, each rounded to one significant figure. To find the maximum perimeter of the rectangle, we want to add the maximum amounts from each measurement. We will therefore use the upper bound of the 4cm, which will be 4.5cm and the upper bound of the 3cm, which will be 3.5cm.
NOTE: I have had many heated discussions with students over my reckless use of 3.5 as the upper bound of 3. Quite rightly students point out that I should use 3.499… There are two reasons I do not.
- This would be really difficult to do especially without a calcuatior.
- 3.499.. is actually the same as 3.5
I know that it feels weird, but for continuous data (data that can be 3.499…) please use 3.5 as the upper bound!
So, the maximum perimeter will be 2 x (3.5 + 4.5) which is 16cm.
If we wanted to find the lowest the area could be, we will now use the lower bounds. 2.5 x 3.5 which will equal 8.75 cm².
Whenever we use subtraction or division, we must think about what we want to be an upper bound and what we want to be a lower bound.
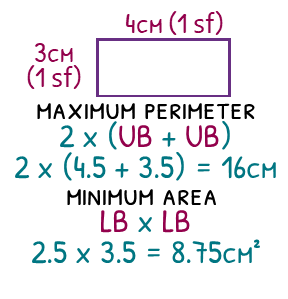
Imagine we have a different rectangle that has an area of 200 m² and a length of 30 m, each to one significant figure. To find the width we will do the area divided by the length, but to find the minimum width, we will not want to use the lower bound for each number. To minimise an answer in a division, we will want to so [smallest possible number] ÷ [largest possible number]. In other words, lower bound ÷ upper bound, or 150 ÷ 35 which equals 4.3 m.
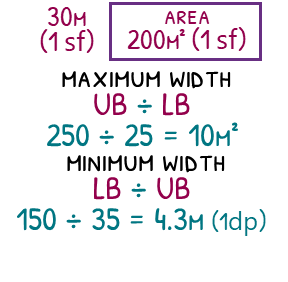
Try our paper on this
Download Accuracy Notes
(Ultimate subscription required)