Angles

Watch this as a video

The basics

Angles on a straight line will always add to make 180 degrees, and angles on a point will add to make 360 degrees.

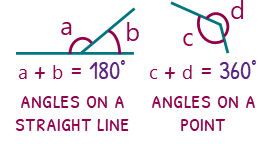
Try our papers on this

Parallel lines

Parallel lines can be shown on diagrams with arrows. When a line travels between the two lines, we get all sorts of wonderful angle facts.

Its important to notice, before we get down to the facts, that the ‘cross’ at the top is identical to the ‘cross’ at the bottom. All the angles at the top have a matching angle at the bottom. These matching angles are called corresponding angles.

Corresponding angles make an ‘F’ shape, a backwards ‘F’ shape, an upside-down ‘F’ shape and an upside-down-backwards ‘F’ shape. The two corresponding angles will always be the same.

Alternate angles are the two acute angles between the lines, and the two obtuse angles. Alternate angles are also equal. In fact, its always a good guess that all the acute angles between parallel lines will be equal, and all the obtuse ones will be equal.

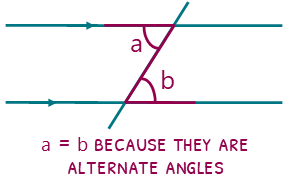
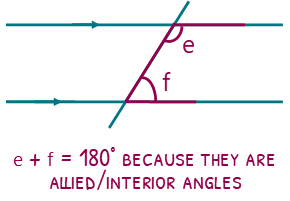
An acute and an obtuse angle between the lines will make allied, co-interior or interior angles (all the maths teachers did have a meeting about this, but sadly we couldn’t agree on a name so you get three). Because these are acute and obtuse they are obviously not equal, but they do add up to 180 degrees which is neat!

Vertically opposite angles are not exclusive to parallel lines, but this seems like a good time to talk about them. When you have two straight lines intersecting, you will end up having two acute angles, and two obtuse. The pairs of angles are equal and we say they are vertically opposite (sometimes you may get away with saying they are simply opposite, but do so at your own risk!)

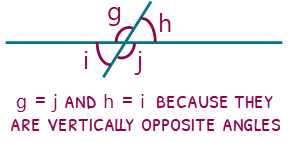
Try our papers on this

Polygons

These are shapes, not what you say when your parrot flies away. There are two types of angles we are interesting in when it comes to polygons: interior and exterior.

Exterior angles are created by continuing the lines of the polygon and measuring the angles they make outside the shape. The beautiful things about these is that in EVERY polygon, they will add to 360 degrees. From a triangle to a googolplexgon, it will still add to 360 degrees.

If you have a regular polygon (all angles are the same), you can do 360 divided by the number of sides to find an exterior angle.

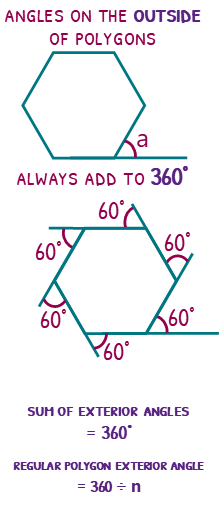
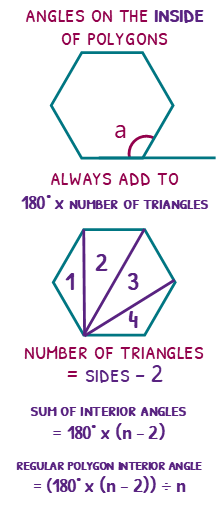
Interior angles are the standard angles inside a shape. To find what they add up to, we first need to find how many triangles you can draw within the polygon.

Pick a corner (vertex) and draw as many lines as you can to other corners. This will make some triangles. Each triangle will contain 180 degrees, so we times the number of triangles by 180 to find the sum of the interior angles.

Drawing triangles in shapes sounds fun, but what do you do if you don’t have the polygon drawn for you? Simple! The amount of triangles you can draw will always be two less than the number of sides in the polygon.

This will give us the formula: sum of interior angles = 180° x (n – 2).

To then find the interior angle in a regular polygon, we divide the sum we found above by the number of sides.

Interior and exterior angles share an important link. They will add to 180 degrees! This means that instead of using the complicated formula to find an interior angle, we can use the nice exterior angle one and subtract it from 180 degrees.

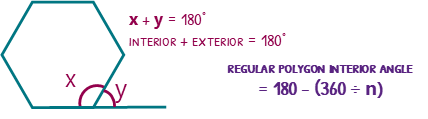
Try our papers on this

Algebra in angles

Algebra can crop up in any topics, but it seems to pair nicely with angle questions.

Below we have an isosceles triangle with angles 3x and 2x and we need to find x. An isosceles triangle will always have two angles the same at the bottom*.

*When I say ‘bottom’ I mean when the equal sides are on the left and right, with the non-equal side at the bottom.

These types of questions require you to find two things.

  1. Find the sum of the angles with algebraic terms
  2. Find the sum of the angles as a number

We have three angles: 2x, 3x and 3x. So as an algebraic term, we have 8x.

We know that the angles in a triangle add to 180 degrees, so our number is 180.

Now we can put these equal to each other (8x = 180) and solve by dividing 8 both sides (x = 22.5°).

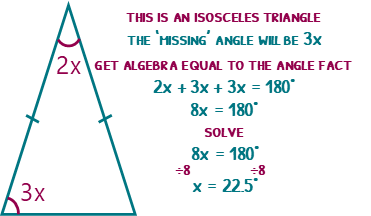
Try our papers on this

Download Angles Notes
(Ultimate subscription required)