Circles
Watch this as a video
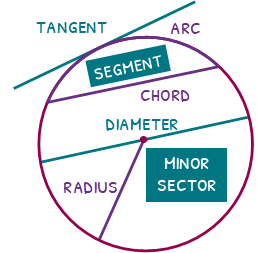
Parts of a circle
Let’s start by talking through the names of the parts of a circle.
The length around a circle is called a circumference. A line from the circumference to the centre is a radius, and if the line carries on across the circle it becomes a diameter. If the diameter does not go through the centre, it is an chord. The chord creates two areas within the circle, the major segment (the big one) and the minor segment (the small one).
A bit of the circumference is called an arc. The area created by two radii (like a slice of pizza) is called a sector. The big sector is called the major sector and the smaller one is called the minor sector. A straight line that skims the outside of a circle at one point is called a tangent.
Circumference
The circumference of a circle is the distance around it. For almost every other shape we would call it the perimeter, but circles obviously have a better marketing team than the other shapes.
To find the circumference there are two formulae. Well actually there is just one, but depending on what the question gives you, it may be helpful to remember two!
If you are given a diameter, such as 10 cm, to find the circumference we simply multiply the diameter by π.
What is π? π (or Pi) is simply a number. Sadly the number goes on forever so we always have to round it. It is roughly 3.14 though.
When we times the 10 by π, we can write our answer as 10π (just like we do with algebra!). If we wanted this as a number, we would use a calculator, or multiply 10 by 3.14, and find the answer is 31.4 cm to 1 decimal place.
If we are given a radius of 20cm, our formula no longer works since it needs a diameter, not a radius. A diameter is always twice the size of a radius. If the radius is 20cm, the diameter will be 40cm. So the circumference will be 40π, or 126cm to 3 significant figures.

Try our papers on this
Half a circle
Circles aren’t always whole, and we could be given a semi-circle, with a diameter of 4cm. The process here is very similar, but all we need to remember is to halve our answer.
We are no longer finding the circumference though, since a circumference must be the full distance around the circle. We are now finding the arc length, since an arc is a bit of the circumference.
We will times the 4 by π but we also must halve it. That will give us 2π, or 6.28cm (3sf).
We can now get a bit more adventurous and find the total perimeter of the semi-circle. We already know the length of the curved bit so we only need to add on the diameter to complete the perimeter. 6.28 + 4 is 10.28cm (3sf).
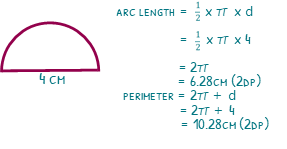
Quarter of a circle
When we are working with quarter circles, we are likely to be given the radius. If the radius is 3cm, we must first double this to find the diameter of 6cm. we can times this by π to find the total circumference of 6π, but we need to divide this by 4 because we have a quarter of the circle. This will give us 1.5π or 4.71cm (2dp).
The perimeter will once again require us to add on the missing bits. The quarter circle has two radii to add on to the arc we have already worked out. 4.71 + 3 + 3 will give us a perimeter of 10.71cm (2dp).
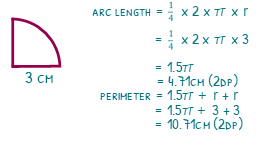
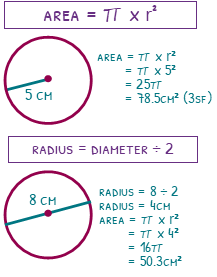
Area
The area of a circle also has a nice simple formula. This time, we need to have a radius, not a diameter. To find an area we square the radius then times it by π.
If the radius of a circle is 5, we will square it, to make 25 then times it by π giving us 25π, or 78.5cm² (3sf).
If we are only given a diameter of 8cm, then we halve it first to give us 4cm, then square that to make 16, and times it by π giving us 16π, or 50.3cm² (3sf).
Try our papers on this
Area of half a circle
If the diameter of the semicircle is 6cm, we will first of all need to find the radius by halving the diameter. We will square the radius (the 3) to make 9 and times it by π to give us 9π. We have half a circle, so we then divide it by 2 to give the answer of 4.5π, or 14.1cm² (3sf).
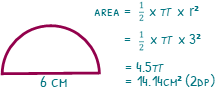
Area of quarter circle
If we have the raius of a quarter circle as 8cm, we can use the formula to find the total area of the full circle. Square the 8, to give us 64, then times by π to give us 64π. We have a quarter of the circle, so we will divide this by 4, to make 16π, or 50.3cm² (3sf).
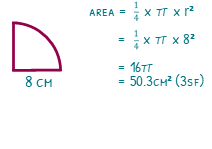
Area of Sector
We have found the area of a full circle, a half circle and a quarter circle, but it is quite simple to find the area of a circle that has any angle. To do this, we need to find two things. The area of the circle and the fraction of the circle we have.
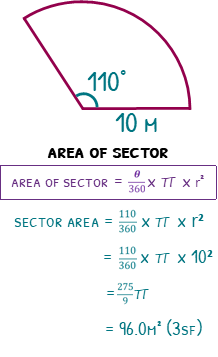
If we have a sector with angle 110°, and a radius of 10m, we can start by finding the fraction of the circle we have. All circles add up to 360°, and we have 110°. So we can divide 110 by 360, giving us 0.30555… (or we can just leave it as a fraction).
To find the area of the full circle, we can square the radius to give us 100, then times it by π to get 100π.
We can then times the fraction of the circle we have by the area of the full circle. 110 over 360 times 100π, which will give us (275÷9)π, or 96.0m² (3sf).
Arc length
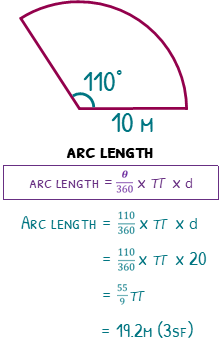
We can also find the length of the arc on the sector with angle 110°, and a radius of 10m. The process is the same. Find the angle and times it by the full circumference.
The angle is 110 over 360, the circumference is 20π. The arc length will therefore be (110÷360) x 20π, giving us (55÷9)π, or 19.2m (3sf).
Find the sector angle
We can finish this topic with a bit of fun. If we know the sector area is 40π and the radius is 20cm, we can find the sector angle.
Always start by writing the formula, then filling in the bits you know.
Sector area = (angle over 360) x π x r².
40π = (x over 360) x π x 20².
We can divide the π both sides to get rid of them. We can then divide the 20 squared (or 400), giving us 0.1 = x over 360. Times both sides by the 360, to give us x = 36.
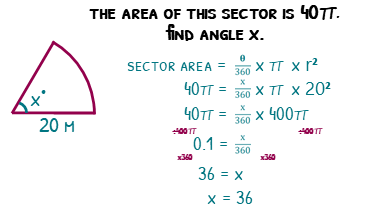
Try our papers on this
Download Circles Notes
(Ultimate subscription required)