Factors, multiples and primes
Watch this as a video
Factors
Factors are the numbers that ‘go into’ a number. The simplest way of finding factors is by starting off asking yourself what times-tables the number is in. We can make sure we do not miss any out by being systematic.
To find the factors of 12, we always start with 1 x 12 (so 1 and 12 are factors). Next we see if 2 goes into 12. 2 x 6 is 12, so 2 and 5 are also factors. Next we move on to 3. 3 times 4 is 12, so 3 and 4 are factors. We do not continue since the next would be 4 x 3, but we already have counted these!
So the factors of 12 are 1, 2, 3, 4, 6 and 12.
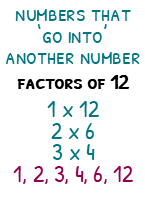
Multiples
Multiples describe the times-table of a number. So the first four multiples of 8 are 8, 16, 24 and 32. Unlike factors, every number has an infinite amount of multiples (because you can always add the number on to find more).
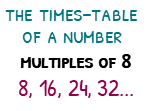
Primes
When looking at factors we found out that every number has a factor of one and itself. What makes prime numbers special is that these are the only factors they have.
7 is a prime number because it is only in the 1 times tables and the 7 times tables. 9 looks like it might be a prime number, but you can find it in the 3 times table, so 9 is not a prime number.
Confusion often ensues when discussing the first prime number. Many student have made compelling arguments that 1 should be classified as a prime number. Unfortunately modern mathematics breaks apart if one is included in the prime club, so the smallest prime number is 2. 2 is also the only even prime number since all other even numbers have 2 as a factor.
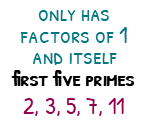
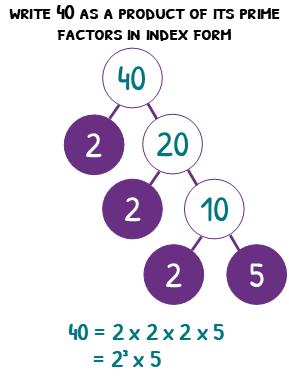
Product of prime factors
We know primes, and we know factors, so why not smash them together to make prime factors. All numbers can be written as a product of their prime factors. To find the prime factors of a number there are a number of different methods, but each are effectively doing the same thing. I like the bubble approach, but if you like straight lines there are better methods out there for you.
To write 40 as a product of its prime factors, start by putting 40 in a circle. Every time we have a number in a circle, we are looking to split it up into two numbers that multiply together to make the number. I would advise you start with seeing if 2 works first, then 3, then 5.
We can split 40 into 2 and 20 (because 2 x 20 = 40), so we show these in circles below. 2 is a prime number so we can leave this, but 20 is not so we will focus on this next. 20 is 2 x 10, so again, we include these circles below.
10 can be split into 2 and 5, because 2 x 5 is 10. Adding these circles, we notice that both 2 and 5 are both prime numbers. When this happens, we can stop!
The prime numbers we found were 2, 2, 2 and 5. Written as a product (product means multiply), the answer would be 2 x 2 x 2 x 5. Often you will be asked to write this in index form. This would give us 2³ x 5.
Try our paper on this
Highest common factors
Highest common factors, or HCF for short, are exactly what you would expect them to be. They are the largest factors that two numbers share. The common factors of 16 and 24 are 1, 2, 4 and 8, so the HCF is 8.
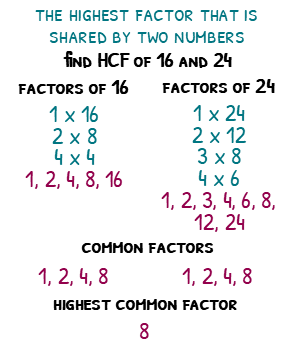
Lowest common multiples
Lowest common multiples, or LCM, are the smallest multiples two numbers share. The LCM of 6 and 9 is 18, since if you write out both times-tables, this is the number you will find both have in common first. You can always multiply this number by 2, 3, 4, etc to find other common multiples.
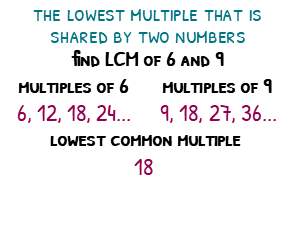
Application
A skill you will need to practise involves spotting when you need to use HCF and LCM within a question.
We have two busses, bus A leaves every 12 minutes and bus B leaves every 16 minutes. If both busses start at 9:00, when will they both leave at the same time again?
At 9:12, bus A will leave again, but bus B will leave 4 minutes later. It seems like it’s going to be tricky to find out when they will both leave. Not so much actually, since this is secretly a LCM question. The LCM of 12 and 16 is 48, so every 48 minutes they will leave at the same time. This will first happen at 9:48.
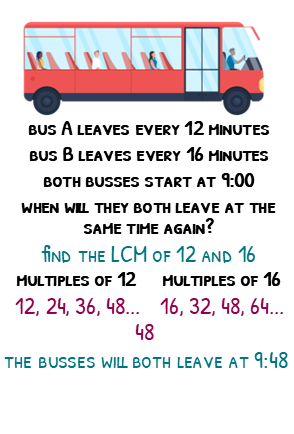
Using prime factors
Using the skills you have gained so far, finding the LCM and HCF is pretty simple, but does take a while, especially as the numbers get bigger. As mathematicians we are always trying to find quicker methods!
We can actually find LCM and HCF using a Venn diagram. The nice thing about this method is it can be very quick for large numbers.
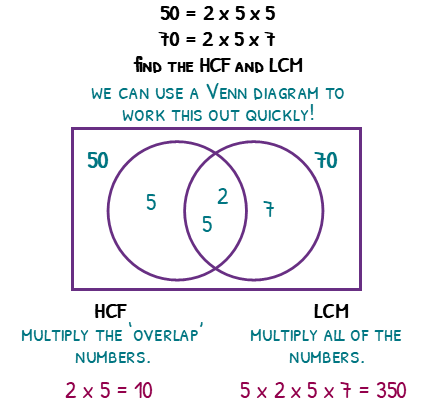
Let’s find the HCF and LCM of 50 and 70.
First we will write both of these as the product of their prime factors. 50 = 2 x 5 x 5 and 70 = 2 x 5 x 7. Next we will draw a Venn diagram with these prime factors. We can see they both have a 2 and 5 so these will go in the middle. 50 then has a left-over 5, and 70 has a left-over 7, so we will add these to the Venn as well.
The HCF can be found by multiplying the numbers in the overlap together. 2 x 5 = 10, so the HCF is 10.
The LCM can be found by multiplying all of the numbers in the Venn diagram together. 5 x 2 x 5 x 7 = 350, so the LCM is 350. A student once asked me “Why doesn’t this just give us the same number as 50 x 70”, and it for some numbers it will. But don’t forget, with the Venn diagram if they both share a number, we only write it once!
Try our paper on this
Download Factors, multiples and primes Notes
(Ultimate subscription required)