Laws of indices

Watch this as a video

Law 1

When you multiply powers with the same base, you add the indices.

Um… OK… what is a base and what are indices? The base is the big number and the index is the little number. 5³ has a base of 5 and a index of 3.

Law 1 states that if we have a to the power of 3 and multiply it by a to the power of 2, we can add the indices (3 + 2) because the bases (the a’s) are the same. Why does this work though?

a cubed is the same as a x a x a and a squared is the same as a x a. Multiplying them together will therefore make a x a times a x a x a, which will be a to the power of 5!

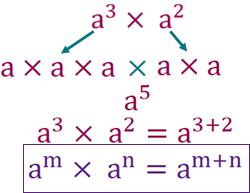
Law 2

When you divide powers with the same base, you subtract the indices.

a to the power of 4 divided by a to the power of 2 will therefore be a to the power of 4 – 2, which is 2.

To see how this works we need to remember that a division can be written as a fraction. a to the power of 4 over a to the power of 2. this will give us a x a x a x a over a x a. We can cancel two a’s from the top and bottom, giving us a x a, or a to the power of 2!

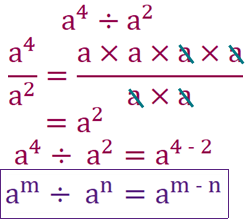
Extras

Having never gone to law school, I am unsure whether the next two count as laws but they are really important for you to remember.

Any number to the power of one is itself. This can be really helpful when you are working with the other laws.

$$a^4\div a$$

To simplify the expression above it might help to rewrite it as:

$$a^4\div a^1$$

Now we use the law and subtract the powers to get a to the power of 3.

If you take ONE THING from reading this, please let it be that ANYTHING to the power of zero is ONE. For some reason examiners LOVE testing this. I imagine they know that many, many students will still write zero as the answer…

Try our papers on this

Law 3

When you have a power inside and outside a bracket, multiply the indices.

a to the power of 3 can be rewritten as a x a x a, so (a to the power of 2) to the power of 3 can be rewritten as (a to the power of 2) x (a to the power of 2) x (a to the power of 2). Using law 1, we will do 2 + 2 + 2, or 2 x 3. 2 x 3 = 6.

Law 3 states we do not need to go through this long process, we can simply multiply the indices together.

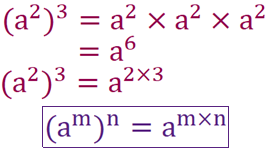
Law 4

When a fraction is the base to a power, the numerator and denominator are raised by that power.

a over b to the power of 3 is the same as a over b x a over b x a over b. We can multiply the tops and bottoms of the fractions to give us a cubed over b cubed.

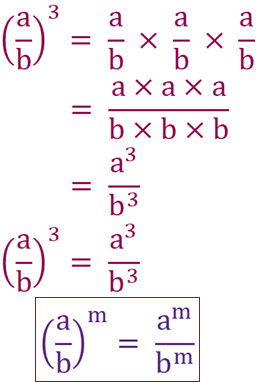
Law 5

When an index is negative, find the reciprocal of the power.

a squared divided by a to the power of 4 will give us a to the power of -2 using law 2. If we write the expression as a fraction, we can see it also gives us 1 over a squared.

If we have a fraction to the power of a negative, we can make the power positive by flipping the fraction. 2 over 3 to the power of -2 would become 3 over 2 to the power of 2. We can then use law 3 to square the top and bottom to give us 9 over 4.

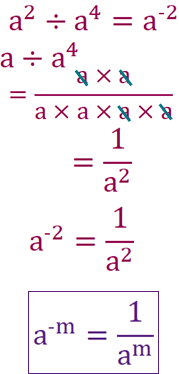
Coefficients

All the laws we have discussed can work alongside coefficients (such as the 3 in 3a).

If we have powers in a fraction, make sure you simplify the numerator and denominator first, before dealing with the division.

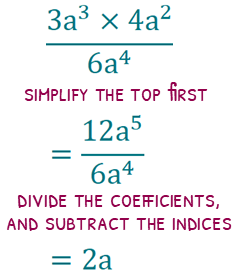
If we have a coefficient inside a bracket, don’t forget that the coefficient MUST also be raised to the power outside the bracket.

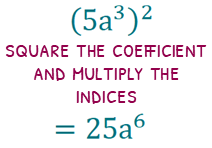
If we have a bracket full of lots of variables, I personally go from left to right dealing with them one at a time.

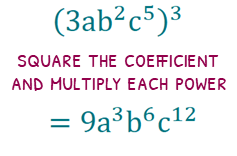
Try our papers on this

Fractional indices (higher only)

When coding the questions for this site, I was left frustrated because there was a nice power function but no rooting function to make the questions with. Ironically, I was making questions for this very topic, and I realised you can work out roots with powers!

To find a square root of a number, you can do that number to the power of a half. Try it now on your calculator. 64 to the power of a half is 8. 121 to the power of 0.5 is 11. How cool is that.

This also works for any root. 8 to the power of a third is the same as cube root of 8, which is 2.

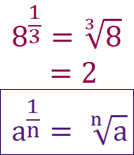
We can mix this law with the others, and find 64 to the power of minus 2 over 3. The negative will mean we will have a fraction with 1 on the top, the 3 will mean we will cube root 64, then the 2 will mean we will then square it. This will give us the answer of 1 over 16.

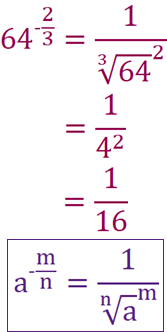
Try our papers on this

Download Laws of indices Notes
(Ultimate subscription required)