Percentages
Watch this as a video
Converting percentages
Before starting its important to understand what percentages are. The truth is that the world would work fine with only having fractions, decimals or percentages.
Fractions are great for precision, with numbers not needing to be rounded, such as a third.
Decimals are fantastic at comparing and are simple to use.
Percentages are very similar to decimals, but instead of having the meaty digits trapped behind a decimal point, they are shown as whole numbers. Newspapers, for example, love percentages. Take a look at a newspaper and see how many times they use percentages compared to fractions and decimals.
The decimal-percentage relationship is beautifully simple, since you only need to multiply a decimal by 100 and you have a percentage! Inversely, to get from a percentage to a decimal, just divide it by 100.
Fractions can be a bit more difficult to convert, but if you know a little Latin, you will know that percent is short for per centum meaning per hundred. OK, I don’t know Latin, and only know cent from USA currency and rapper 50 cent.
Since percent means per hundred, all we need to do to convert a fraction to a percentage is make sure the denominator is 100. Once we have done this, the numerator becomes the percentage.
To convert a percentage to a fraction, simply put the percentage over one hundred.
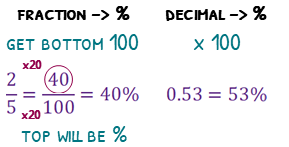
Make a percentage
Percentages can be used to describe what proportion something is comparted to the whole. If there are ten balls and three are red, we can find the fraction of red balls first.
Put the number of red over the total amount of balls, or 3 over 10. Next, make this a decimal by dividing the fraction, then multiply it by 100 to make it a percentage. This will give us 30%.

Try our paper on this
Percentage of an amount
Be prepared, you will be asked to do this a lot! There are two different methods, with a calculator or without.
Let’s work out 17% of £600.
If you have a calculator you can convert the percentage into a decimal by dividing by 100, then multiply this by the amount. 17 divided by 100 is 0.17, then 0.17 times 600 is £102. Simple.
Without a calculator, we can break the 17% into much nicer pieces. 17% is 10% + 5% + 2%. To find 10% we can divide the 600 by 10, giving us 60. We can half this to find 5%, giving us 30. We can divide the 600 by 100 to find 1%, which will be 6, but then double it to find 2%, giving us 12. We can then add the 60, 30 and 12 together to give us, you guessed it, £102. Not as simple, but way more satisfying!
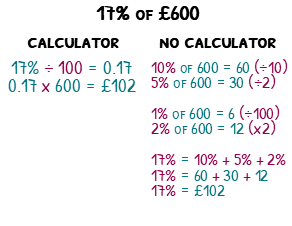
Try our paper on this
Increase and decrease by a percentage
To increase 40g by 24% without a calculator, we would find 24% using the previous method which will be 9.6g, then add it on to the 40g to give us 49.6g.
To understand percentages fully you must understand multipliers and we can use this with the calculator method.
To find the multiplier we always start with 100%. This 100% represents our original amount (the 40g). Next, we ask ourselves what are we doing to this original amount. In this question, we are increasing it by 24%. Let’s do this then, 100% + 24% will be 124%.
We have already established that percentages are pretty rubbish at doing calculations so like we always do we next have to convert this percentage into a decimal by dividing by 100. 124 divided by 100 is 1.24.
The 1.24 is our multiplier. Its a pretty powerful thing! If you multiply anything by 1.24 it will instantly add 24% to it without you having to lift a finger.
It just so happens we want to raise 40g by 24% so all we need to do is plug in 40 times 1.24 into our calculator and read off the answer of 49.6g. Some students panic at this stage and feel this is too simple. Fret not, it really is that simple!

Try our paper on this
- Increasing And Decreasing By Percentages Paper (foundation)
- Increasing And Decreasing By Percentages Paper (higher)
Percentage change
If a business buys something for £45 and sells it for £67 they can calculate their percentage increase, or percentage profit. They would work out their profit (the change) by subtracting the values, giving £22, then divide by the original amount giving 0.488… This is their answer as a decimal, so we need to multiply it by 100 to make it a percentage of 49% to the nearest percent.
When working out percentage change, always remember the formula of change over original times 100%. This could be a percentage increase or decrease, but make sure you always divide by the original amount.
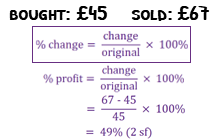
Reverse percentages
Imagine you are staring at the TV of your dreams, admiring that it has 28% off and is now only £396. The mathematician inside you starts stirring, and you start to wonder what the price was before the discount.
Reverse percentages require you to have excellent understand of percentages, which if you have read this page from the start you will have!
We will cover two different methods of finding the original amount.
Method 1
We can find the original amount by dividing the final amount by the multiplier (doing the opposite of what we did earlier). Finding the multiplier always starts us at 100%. This time we have to imagine what the shop did to this price before we walked into the shop. They subtracted 28% from it. So 100% – 28% is 72%. To convert this to a multiplier (or decimal) we divide it by 100, giving us 0.72.
We could now multiply anything by 0.72, and it will automatically decrease it by 28%, but this question is working backwards. We need to divide the £396 by 0.72 to find out the original price, which will give us £550.
Method 2
If you are not in a multiplier mood, then let’s give you an alternative method. We discussed in method 1 that a 28% reduction in price means that the £396 represents 72% of the original price. We can use that to divide the 396 by 72 to find 1% of the original price, giving us 5.5. We can then multiply this by 100 to give us the original price of £550.
We can check our answer of £550 decreasing it by 28%, and we can smile when we find the answer of £396.

Try our paper on this
- Percentage Change and Reverse Percentages Paper (foundation)
- Percentage Change and Reverse Percentages Paper (higher)
Interest
When you put money in a bank, the bank will give you a percentage of that money each year as interest (unless the interest rate is 0%). They get this money by using you money to lend to others with loans or mortgages.
Imagine we have two banks, each willing to give us 5% interest on our £380, and we would like to keep our money in the banks for 4 years. The only difference between the banks is one uses simple interest and the other uses compound interest. Which should we pick?
99.9% of interest you will deal with in your life will be compound interest, so let’s get the simple interest out the way first.
Simple interest
Simple interest pretends the bank only cares about the money you had in the account on day 1. They use this amount to calculate the amount of money they will give you each year for the rest of time.
So the simple interest bank will find 5% of 380, which is £19, then multiply that by 4 for each year. This gives us £76. We then add this to the amount we put in giving us a final account amount of £456.

Compound interest
This is so common, that we normally just call this interest. Compound interest is calculated each year. This means that the interest you received in year 1 will make you interest in year 2 even bigger.
To calculate compound interest, we first find the multiplier. We start with 100% and the bank is giving us 5%, meaning we get 105% each year. Divide this by 100 to find the multiplier (or decimal) of 1.05.
Any time we would like to increase something by 5% we can multiply it by 1.05. This is handy, because we want to do this four times to the £380. We could do £380 times 1.04 times 1.04 times 1.04 times 1.04 or even better, £380 times 1.04 to the power of 4. Either will give us £461.89.
We can see that we should never use the simple interest bank if the terms are the same, with the compound interest bank giving us £5.89 more.
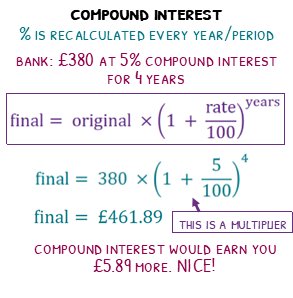
Depreciation
Depreciation uses exactly the same method as compound interest, with the only difference being it is a decrease.
If a £24000 car loses 15% of its value each year, and we are asked to find its price after 6 years, we can use multipliers to find the answer relatively qucikly.
100% – 15% gives us 85%, then divided by 100 we have a multiplier of 0.85.
We can then get our 24000 and multiply this by 0.85 six times, or do 24000 times 0.85 to the power of 6. Either way we get our price of £9051.59.
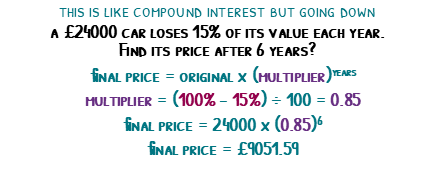
Try our paper on this
Download Percentages Notes
(Ultimate subscription required)