Ratios
Watch this as a video
The basics
Imagine I know that you have twice as many apples as me. If all of my apples filled one box, all of your apples would fill two.
We can compare my amount of apples to yours in the ratio 1 : 2.
Instead of boxes, we can call the bits of the ratio ‘parts’. So the ratio is 1 part : 2 parts.
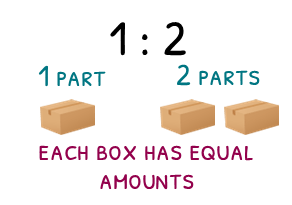
Simplify
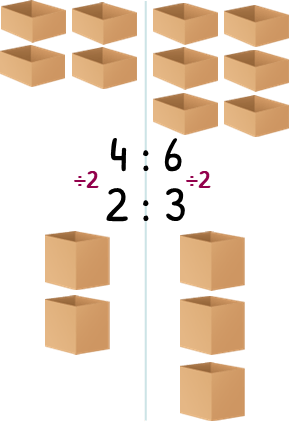
What happens if I buy boxes that are half the size. My apples will now fill two boxes, and yours will fill 4. The ratio is now 2 : 4. We call this an equivalent ratio, which is a fancy way of saying the same.
Simplifying a ratio is very similar to simplifying a fraction. You are looking to keep dividing each side of the ratio until you cannot go any further.
In the ratio 20 : 30, we can divide both sides by 10 to make 2 : 3.
Tricky simplifying
If both ratios are decimals, multiply them by a power of 10 to make them both whole numbers.
We can multiply 0.6 : 0.9 by 10 to make 6 : 9. We can then divide by 3 to give our answer 2 : 3.
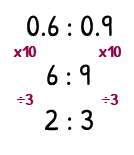
If the two sides of the ratio are different units, convert them into the smaller unit before simplifying.
To simplify 5m : 300cm we would start by converting it to 500cm : 300cm, then divide by 100 to get 5 : 3. Ratios work for all units, so we do not need the units anymore.
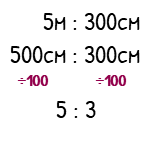
Sometimes you will be asked for a unit ratio, meaning you will need to make one of the sides have 1 part.
To convert 5 : 21 as a ratio of 1 : n, divide both sides by 5 to give 1 : 4.2
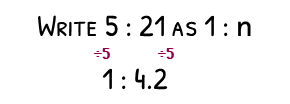
Try our paper on this
- Simplifying and Multiplying Ratios Paper (Foundation)
- Simplifying and Multiplying Ratios Paper (Higher)
Fractions
Fractions always compare one item to the whole, whilst ratios normally compare two or more items to each other.
To convert a ratio to a fraction, you must make sure the denominator includes all the parts in the ratio.
In the ratio 2 : 3, the fraction of the left-hand side will be 2 over 5 and the fraction on the right-hand side will be 3 over 5.

Part : whole
Very rarely you may come across a ratio written where the left-hand side represents an item, but the right-hand side represents the whole.
For example, the ratio or cats to pets is 2 : 5.
Cats are a pet, therefore are included on the left AND right hand side.
If we wanted to make this a fraction of cats to non-cats, we can remove the cats from the right hand side to make the ratio 2 : 3.

Try our paper on this
- Convert to Fractions and Unit Ratios Paper (Foundation)
- Convert to Fractions and Unit Ratios Paper (Higher)
Sharing
Imagine that each part in a ratio is a box, and all boxes MUST have the same amount of stuff in them.
If we wanted to split £50 in the ratio 2 : 3, we can represent the ratio as 2 boxes on the left and 3 on the right.
The first step is to figure out how many boxes, or parts, we have in total. 2 + 3 will mean there are 5 boxes. Nice!
I have £50 to give to all the boxes, but each box MUST contain the same amount. To calculate the amount in each box, we divide the 50 by 5, giving us £10 to put in each box.
Finally, lets put the money in each box. We had 2 boxes on the left, each with £10 in, so 2 x £10 = £20. On the right, we have 3 boxes, which will by 3 x £10 = £30.
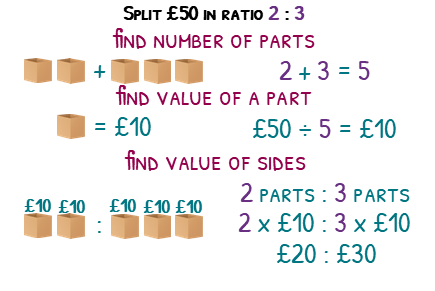
Tricky sharing
Cheese is split between three boxes A : B : C in the ratio 2 : 4 : 5.
C has 15kg more than A. Find the amount in box B.
Our goal for these types of questions is to find the amount for each part, but we no longer have the total amount.
This is not a problem though since we know C has £15 more than A. C has 3 more boxes than A. So the 3 boxes contain 15kg.
15kg divided by 3 is 5kg, meaning each box contains 5kg of cheese.
B has 4 parts, so 4 x 5kg is 20kg.
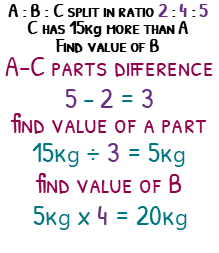
Given quantity
Anne and Ben split money in the ratio of 5 : 6. Ben has £18. Find the amount Anne has.
Going back to our boxes, Anne has 5 boxes, Ben has 6. We know Ben has £18 split among his 6 boxes. £18 divided by 6 gives us £3 in each of Ben’s boxes.
The boxes in ratios ALWAYS have the same amount, so Anne’s 5 boxes will each have £3 in. 5 x £3 = £15. Anne has £15.
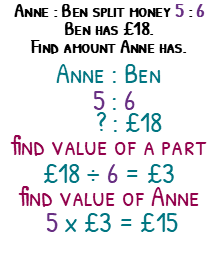
Try our paper on this
Download Ratios Notes
(Ultimate subscription required)