Solve linear equations

Watch this as a video

Basics

You will see the word ‘solve’ a lot in your mathematical travels, but what does it mean? Put simply, solve means find the value of the letter. If the letter is x, your target will be to get ‘x = something’.

When we solve equations, we first need to understand inverse operations. This is a fancy way of saying the opposite.

The inverse of add is subtract and the inverse of subtract is add. The inverse of multiply is divide and the inverse of divide is multiply.

When we solve equations, we are looking at doing the inverse of everything that is done to the letter.

To solve x + 3 = 12, the x has 3 added to it, so must do the inverse of ‘add 3’. This will be ‘subtract 3’. When we subtract 3 from the left-hand side, we are just left with x. Nice! When we do it to the right-hand side we are left with 9. We have x = 9. We have solved!

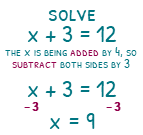
Solving x – 3 = 12 will involve the same steps. This time we have ‘subtract 3’, so we will ‘add 3’ both sides. x = 15.

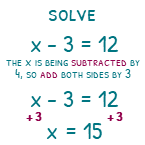
3x = 12 seems harder to solve, but ask yourself what is happening to the x. 3x means 3 times x. The x is being multiplied by 3. What is the inverse of ‘times 3’? ‘divide 3’ of course! So we divide the left-hand side by 3, to give us x, then the right-hand side to give us 4. x = 4.

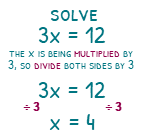
To solve x over 3 = 12 we must first remember that ‘over 3’ just means ‘divide 3’. The inverse will therefore be ‘times 3’. 12 times 3 is 36. x = 36.

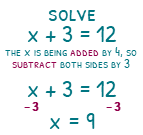
Try our paper on this

Two operations

We can combine what we learnt in the last section to solve equations that have two operations.

5x + 3 = 18 has a ‘times 5’ and an ‘add 3’. But which should we deal with first to solve it? A simple way of remembering is that we deal with them the opposite way around to BIDMAS/BODMAS. This would mean we tackle the ‘add 3’ first.

When we ‘subtract 3’ both sides we are left with 5x = 15, which we can then ‘divide 5’ both sides to find that x = 3.

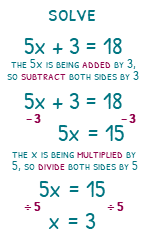
x over 3 minus 2 = 4 will work in the same way. Reverse BIDMAS/BODMAS means we will deal with the ‘subtract 2’ first, so ‘add 2’ both sides. Then we deal with the ‘over 3’ by doing ‘times 3’ both sides. x = 18

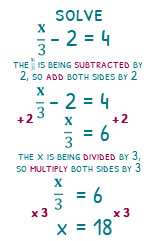
Function machines

Functions machines are a graphic way to show what we have done in the previous sections. 3x + 6 will create a function machine of ‘times 3’ then ‘add 6’.

If we feed in an input of 2, we will ‘times 3’, giving 6, then ‘add 6’ giving us an output of 12.

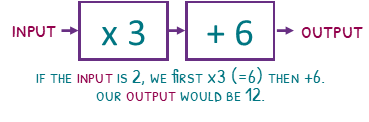
Function machines get interesting when we are given the output and are asked for the input. We will need to find the inverse of the operations. ‘times 3’ will become ‘divide 3’. ‘add 6’ will become ‘subtract 6’.

If we feed in an output of 36, we will then ‘subtract 6’, giving 30, then ‘divide 3’ giving an output of 10.

Try our paper on this

Brackets

When you have brackets, always get rid of them first!

To solve 3(2x + 5) = 57, expanding the brackets gives us 6x + 15 = 57. We will then ‘subtract 15’ both sides, giving us 6x = 42. Finally we will ‘divide 6’ both sides giving us x = 7.

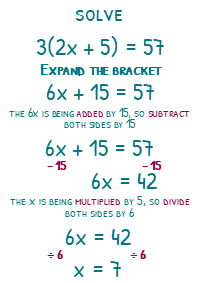
Fractions

If the x term is trapped in a fraction, always get rid of it first!

To solve (3x + 4) over 2 = 11, we need to get rid of the ‘over 2’ before doing anything else. To do this we can ‘times 2’ both sides. The left-hand side will just become the numerator of the fraction, so 3x + 4. The right-hand side will become 22, giving us 3x + 4 = 22. Now we can ‘subtract 4’ both sides, giving us 3x = 18, then ‘divide 3’ both sides giving us the answer of x = 6.

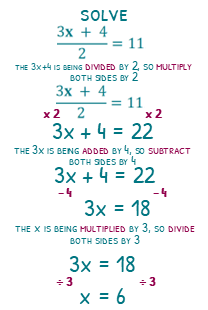
Letter on both sides

If there are x terms on both sides, always deal with this first!

It is easy to start getting confident with solving equations, only to have your confidence knocked when you find a question that has x on both sides.

To solve 5x + 3 = 3x – 15, we need to figure out which of the x terms will be easier for us to deal with. The simplest way of doing this is look at which is smaller. Here, we have a 5x and a 3x, so we will focus on the 3x. We want to remove the 3x from the right-hand side. To do this, we will ‘subtract 3x’ both sides. This will give us 2x + 3 = -15. We now have a nice 2-operation equation to solve! ‘subtract 3’ both sides, giving us 2x = -18, then ‘divide 2’ both sides, giving us the answer of x = -9.

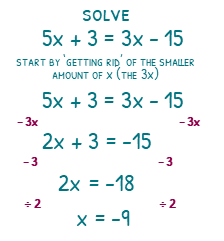
To solve 10(x – 3) = -2(x + 3), we need to first of all expand the brackets. This will give us 10x – 30 = -2x – 6. The smaller x term is -2x. To get rid of -2x, we will need to ‘add 2x’ to both sides. This will give us 12x – 30 = -6. ‘Add 30’ both sides will give us 12x = 24, then ‘divide 12’ both sides to give us the answer of x = 2.

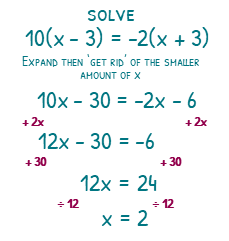
Worded problem

Solving equations can be used to find real-world solutions to problems you may have.

“Twice a number is equal to six more than that number”

Let’s pick apart this question to convert it into an equation, then solve it!

First of all, we have an unknown number in this question, so we can call this unknown number x.

‘Twice a number’ will be 2x.

‘is equal’ means we can use an = sign.

‘ six more than that number’ mean x + 6.

2x = x + 6.

‘Subtract x’ both sides, to give us x = 6.

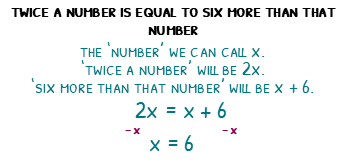
Try our paper on this

Download Solve linear equations Notes
(Ultimate subscription required)